Nota: En la entrada “Tipos de números” en esta misma web encontrarás las definiciones de tipos de números utilizadas aquí.
Si le preguntas a varios especialistas ¿A qué es igual pi? podrían responderte:
Un ingeniero: Es aproximadamente igual a 3+1/7
Un físico: Es 3,14159
Un matemático: (después de pensarlo un poco) es igual a π
Bromas aparte, el ser humano ha concebido la proporción entre la longitud de la circunferencia y su diámetro de distintas formas a lo largo de la historia.
- Primero fue el número entero 3
- Después fue sucesivamente uno de los siguientes racionales 22/7, 223/71, 377/120, 355/113 y otros
- También, a principios del siglo XX se construyeron aproximaciones de π que incluían radicales
- Pero hoy sabemos que π no es entero, ni racional ni algebraico
Pero hasta que los matemáticos no formalizaron las definiciones de límite y de infinito no obtuvieron valores satisfactorios de π.
- El número π pasó a ser una fracción continua del tipo
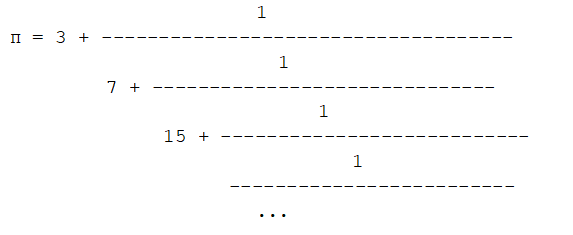
- Matemáticos como Halley, Leibniz, Euler, Taylor y otros expresaron π como distintas sumas de infinitos sumandos (véase la entrada “Calcule usted mismo pi”).
Pero seguían empeñados en conseguir un valor exacto de π, hasta que demostraron que
- π no es un número racional, es decir no se puede expresar como cociente de dos número enteros; por tanto π es irracional
- π no es un número algebraico, es decir no es raíz de ningún polinomio con coeficientes enteros; por tanto π es transcendente (fue demostrado por Lindemann en 1882)
¿Es π un número Normal?
Un número es normal cuando, en su expresión decimal, cada una de las cifras del 0 al 9, o cualquier conjunto de ellas, aparece en igual número que las/los demás.
A pesar de que el matemático Kanada calculó mil doscientos millones de cifras de π y de que su estudio estadístico dio un valor de repeticiones muy aproximado de cada una de las cifras del 0 al 9, aún no sabemos si π es normal pues por ahora no hay una demostración formal y rigurosa.
A pesar de sospechar que la mayoría de los números irracionales son normales, no se sabe de ninguno, salvo los construidos exprofeso para que lo sean, que sea normal. Este es el caso de pi, del número e, de la raíz de dos, del número áureo, etc.
¿Es π aleatorio?
Si revisamos como aparecen dispuestas las cifras de π nos parecería que claramente es aleatoria su disposición. De hecho π superó todos los test de aleatoriedad al que fue sometido por los hermanos Chudnovsky .
Pero según Kolmogorov, eminente matemático ruso, un número es tanto más aleatorio cuanto más largo es el algoritmo mínimo para calcularlo. Si hacemos caso a Kolmogorov deberíamos sospechar que π no es aleatorio, pues existen algoritmos relativamente cortos que calculan sus cifras.
Si toda la secuencia de dígitos de π fuese aleatoria, entonces π sería un número normal, cosa que no está demostrada.
Y como no hemos encontrado un patrón en la distribución de los números debemos suponer que π es débilmente aleatorio.
A pesar de todo hay quien ha utilizado a π como generador de número aleatorios
¿Es π un número-universo?
Si π fuese un número-universo sería posible encontrar en él cualquier secuencia de dígitos que imaginemos. Y si ideamos un procedimiento para convertir números en letras podríamos encontrar en él cualquier secuencia de letras que pudiéramos concebir.
Y al ser infinita esta secuencia de letras, encontraríamos dentro de π, además de galimatías incomprensibles de letras, el texto completo de “El Quijote”, “Hamlet”, las obras completas de Borges o cualquier artículo o texto escrito previamente por la humanidad.
No sabemos si π es un número-universo, pero sí sabemos que todos los números-universo son normales. Como ejemplo valga el número ideado por David Gawen Champernowne en el siglo XX y que lleva su nombre. Este es:
0,1234567890111213141516171819102122232425262728292….
que, además de ser normal, es trascendente y número-universo.




