En la entrada “Calcule usted mismo el valor de pi” de esta web, se describe como calcular el valor de π mediante aproximaciones por polígonos regulares al perímetro de una circunferencia.
Una vez conocida la fórmula del perímetro de un círculo (2πr), en esta entrada vamos a utilizar un método sencillo y sorprendente para calcular el área de un círculo utilizando aproximaciones sucesivas mediante rectángulos .
Para ello divídase un círculo en un número de sectores circulares iguales como, de manera aproximada, indica la figura
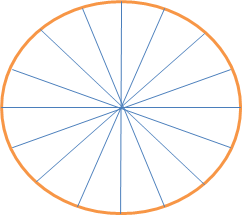
En nuestro ejemplo hemos elegido 16 sectores por claridad en la explicación, pero mientras más sectores se utilicen, más preciso será el cálculo de π.
Dispongamos los sectores uno junto a otro de la siguiente manera
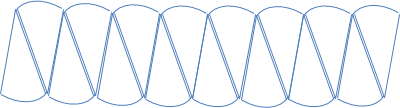
Imaginemos que nuestra nueva figura es un paralelogramo, de hecho se parecerá cada vez más a un paralelogramo según vayamos aumentando el número de sectores en los que dividamos el círculo. La altura de nuestro paralelogramo sería aproximadamente igual a R (el radio del círculo) y su base, 8 veces la cuerda del segmento la cual se aproxima a la mitad del perímetro del círculo, ya que hemos utilizado la mitad de los segmentos circulares para construir la base. Por tanto podemos aproximar la base al valor de πxR
Como la superficie de un paralelogramo es base por altura, la de nuestro hipotético paralelogramo es S = R x π x R es decir S = π x R2
Aumentando el número de segmentos, en los que dividimos el círculo, vamos aproximando nuestro cálculo al valor real, de modo que con infinitos segmentos daríamos en el clavo.
Espero que, aunque poco ortodoxa, esta visión del área de un círculo de, para muchos, sentido a la fórmula πxr2




