Me imagino que usted estará pensando ¿qué tendrá que ver π con el teorema de Pitágoras?
Su duda es lógica pues el número π se relaciona con círculos y el teorema de Pitágoras con triángulos y cuadrados.
Vamos a esbozar aquí una generalización del teorema de Pitágoras en la cual aparece el número π.
Según nos enseñaron en la escuela, y a los más afortunados le demostraron, si sobre los lados de un triángulo rectángulo dibujamos cuadrados, entonces el área del cuadrado dibujado sobre la hipotenusa es igual a la suma de las áreas de los otros dos cuadrados.
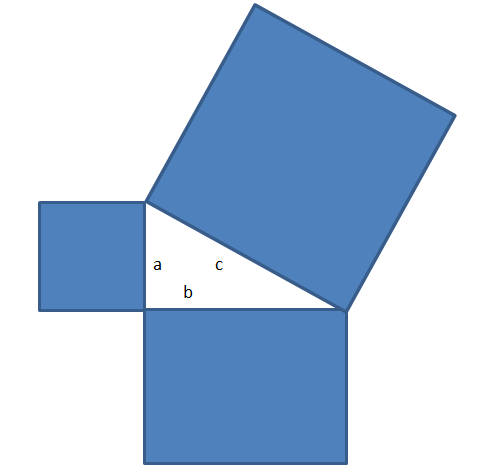
Dejo al lector que se coma la cabeza tratando de demostrar que si sustituimos los cuadrados por polígonos regulares de igual número de lados cada uno podremos afirmar también que el área del polígono dibujado sobre la hipotenusa es igual a la suma de las áreas de los polígonos dibujados sobre los catetos. Como pista, para la demostración, diré que el área de un polígono regular de n lados es igual a la mitad de su perímetro multiplicada por la apotema y que la apotema es igual a la mitad del lado dividida por la tangente de π/n (aparece aquí por primera vez nuestro número π)
Y dando un vertiginoso salto hacia polígonos de infinitos lados, ¿podremos afirmar que el área del semicírculo dibujado sobre la hipotenusa es igual a la suma de las áreas de los semicírculos dibujados sobre los catetos?
(ruego al lector que disculpe mi torpeza a la hora de dibujar semicírculos)
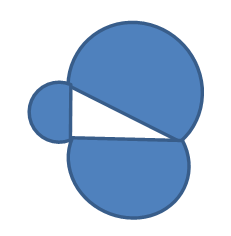
Los radios de estos semicírculos son iguales a la mitad de la hipotenusa y a la mitad de cada uno de los catetos del triángulo. Por tanto el área de cada semicírculo será la mitad de lo que nos indique la fórmula π.r2 en la que sustituiremos r por la mitad de cada lado del triángulo, teniendo así las áreas
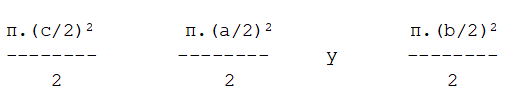
¿se cumplirá aquí también nuestro particular teorema de Pitágoras?
Es decir, ¿será cierto que?
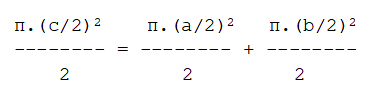
Para comprobar que sí lo es basta partir del teorema de Pitágoras
c2 = a2 + b2
Multiplicando todos los términos por π/4
π.c2/4 = π.a2/4+ π.b2/4
o lo que es lo mismo
π.(c/2)2 = π.(a/2)2 + π.(b/2)2
Nos basta ahora dividir todos los términos por 2 para obtener la fórmula que queríamos demostrar y por tanto que es cierta nuestra generalización del teorema de Pitágoras, en el que una vez más vemos aparecer al número π
¿Qué tal si a nuestro nuevo teorema le llamáramos Teorema de Pitágoras Extendido?
Nota Final:
En esta nota final Pitágoras no tiene nada que ver pero sí π, por lo que aprovecho la ocasión para comentar que como el perímetro de un círculo es π multiplicado por su diámetro, los de nuestros círculos serán π.a, π.b y π.c; por tanto la suma de los perímetros será igual a π.(a+b+c), es decir el perímetro del triángulo multiplicado por π. Conclusión, la suma de los perímetros de nuestros semicírculos es igual a la mitad del perímetro del triángulo multiplicada por π.




